<<
2601.22132v1_Pay_for_Hints_Not_Answers_LLM_Shepherding_for_Cost.pdf

---
## Page 1
[](/attach/4f91145b287ae51d50fb00db9c73a1abd8c4abfaa816d614e134c6b64fbc173e_p001.png)
### 和訳
ヒントにお金払おうや、答え丸ごとに払わんと:コスパ最強の推論のためのLLMシェパーディング
Ziming Dong 1 Hardik Sharma 2 Evan O'Toole 1 Jaya Prakash Champati 1 Kui Wu 1
要旨
大規模言語モデル(LLM)っちゅうのは、めっちゃ複雑な推論タスクで最先端の性能を叩き出すんやけど、推論にかかるコストがえげつなくて、大規模に使おうとすると厳しいねん。一方で小規模言語モデル(SLM)は劇的にコスト削減できるんやけど、精度がだいぶ劣るんよな。今までのアプローチ—ルーティングとカスケーディング—は、LLMを「全部使うか全く使わんか」の二択として扱ってたんや。クエリがLLMを完全にスルーするか、LLMがフル回答を生成してフルコストかかるか、どっちかやねん。ワイらは「LLMシェパーディング」っちゅう新しいフレームワークを提案するで。これはLLMから短いプレフィックス(ヒント)だけをもらって、それをSLMに渡すっちゅうもんや。このシンプルな仕組みが数学とコーディングのタスクでめっちゃ効くんよ:LLMのフル回答のたった10〜30%のヒントでも、SLMの精度がガツンと上がるねん。シェパーディングはルーティングとカスケーディングの両方を一般化してて、オラクル(完璧な判断ができる場合)の意思決定下ではより低コストを達成するんや。ワイらはヒントが必要かどうかと、何トークン要求するかを同時に決める2段階予測器を開発したで。広く使われてる数学的推論(GSM8K、CNK12)とコード生成(HumanEval、MBPP)のベンチマークで、シェパーディングはLLMだけ使う場合と比べてコストを42〜94%削減するんや。最先端のルーティングやカスケーディングのベースラインと比べても、精度を維持しながら最大2.8倍のコスト削減を実現するで。ワイらが知る限り、これはSLMとLLMの協調においてトークンレベルの予算制御を活用した初めての研究やねん。
1. はじめに
大規模言語モデル(LLM)は複雑な推論タスクで最先端の性能を出すんやけど、推論コストが大規模展開の壁になっとるんや。一方で、めっちゃ優秀なオープンソースの小規模言語モデル(SLM)が登場してきて、コスパええ推論の新しいチャンスが生まれてるねん—エッジデバイスでも、プライベートサーバーでも、共有データセンターでも使えるで。SLMには明らかなメリットがあるんや:レイテンシが低い、プライバシーが向上する、お金も電気代もめっちゃ節約できる。せやけど、論理とか数学を扱うタスクでは、SLMとフロンティアLLM(GPTとかGeminiとかClaudeとか)の品質差がまだまだデカいんよな(Subramanianら、2025)。ユーザーや組織は難しいトレードオフに直面するわけや:コスト削減のために劣る回答品質を受け入れるか、精度を維持するためにLLMアクセスにプレミアム料金払うか。
このコストと品質のトレードオフが核心的な問いを突きつけるんや:高価なLLMへの依存を最小限にしながら、SLMの出力品質を大幅に向上させるにはどうしたらええんや?この問いは特にリソースが限られた環境で切実やねん—接続が限られたエッジデバイス、レイテンシにシビアなアプリケーション、コスト意識の高い導入環境—こういうとこでは、LLMを1回呼ぶだけでもかなりのオーバーヘッドになるんや。目標は単に推論を速くすることやなくて、与えられた品質目標に対して根本的にLLMの計算を減らすことやねん。
この課題に対処するために2つの補完的なパラダイムが登場してきたで:ルーティングとカスケーディングや(Beheraら、2025)。ルーティング(Luら、2024;Dingら、2024;Ongら、2025)は学習された分類器を使って、各クエリをちょうど1つのモデルに振り分けるんや—クエリの複雑さに基づいて、SLMが全部処理するか、LLMに転送するかのどっちかやねん。カスケーディング(Chenら、2024;Aggarwalら、2024;Guptaら、2024)は順次的なアプローチを取るんや:まずSLMが回答を試みて、SLMの回答が信頼度や正確性のチェックに失敗した場合にだけLLMを呼び出すねん。
ワイらはルーティングもカスケーディングも根本的な限界を共有してることに気づいたんや:どっちもLLMを「全部か無か」のリソースとして扱ってるんよな。クエリがLLMを完全にスルーするか、LLMがフル回答を生成してLLM推論のフルコストがかかるか、どっちかやねん。この二項対立的な見方は重要な機会を見落としてるで:ほとんどのLLMサービスプロバイダーはユーザーがmax_new_tokens(出力トークン数のユーザー定義上限)を指定できるようにしてるんや。この機能を戦略的に活用すれば、LLMコストを削減しながら同時にSLMの回答品質を向上させることができるねん。
ワイらは「LLMシェパーディング」を提案するで。これは部分的な
---
## Page 2
[](/attach/4f91145b287ae51d50fb00db9c73a1abd8c4abfaa816d614e134c6b64fbc173e_p002.png)
### 和訳
LLMシェパーディング
(a) プロアクティブ・シェパーディング
(b) リアクティブ・シェパーディング
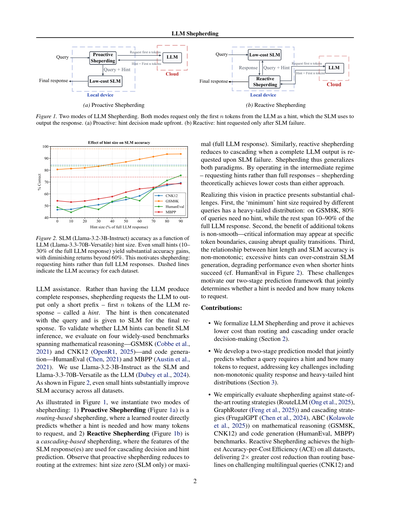
図1. LLMシェパーディングの2つのモードやねん。どっちのモードもLLMから最初のnトークンだけ「ヒント」としてもらって、そのヒントを使ってSLM(小さいモデル)が回答を出すっていう仕組みやで。(a) プロアクティブ:最初からヒントが必要かどうか決める方式。(b) リアクティブ:SLMが失敗してからヒントをお願いする方式。
---
このシェパーディングっていうのはな、LLMにフル回答させたら「極大」になるから、ヒントゼロ(SLMだけ)か極大かの両極端やねん。同じようにリアクティブ・シェパーディングも、SLMがコケた時にLLMのフル回答もらったらカスケーディング(段階処理)と一緒になるわけや。せやからシェパーディングは両方のやり方を一般化してるねん。フル回答やなくてヒントだけもらうっていう中間のやり方やから、理論的にはどっちのアプローチよりもコスト安くなるはずやねん。
ただな、これを実際にやろうとするとめっちゃ難しい問題があるねん。まず、クエリによって必要な「最小」ヒントサイズがバラバラで、裾野の重い分布になってるんや。GSM8Kでいうと、80%のクエリはヒントなしでいけるんやけど、残りは LLMフル回答の10〜90%のヒントが必要になるねん。次に、トークン増やした時の効果がなめらかちゃうねん。重要な情報が特定のトークンの境目にドカンと出てくるから、品質がガクンと変わるポイントがあるんや。ほんで3つ目、ヒントの長さとSLMの正解率の関係が単調ちゃうねん。ヒント多すぎるとSLMの生成を縛りすぎて、短いヒントで成功してたのに逆に性能落ちることもあるんや(図2のHumanEval見てみ)。こういう課題があるから、ヒントが必要かどうかと何トークン要求するかを一緒に予測する2段階の予測フレームワークを考えたんや。
**貢献ポイント:**
• LLMシェパーディングを形式化して、オラクル(神様視点)の意思決定やったらルーティングやカスケーディングよりコスト低くなるって証明したで(セクション2)。
• クエリにヒントが必要かどうかと何トークン要求するかを同時に予測する2段階予測モデル作ったで。非単調な品質応答とか裾野の重いヒント分布とかの課題にも対応しとるで(セクション3)。
• シェパーディングを最先端のルーティング戦略(RouteLLM (Ong et al., 2025)、GraphRouter (Feng et al., 2025))とカスケーディング戦略(FrugalGPT (Chen et al., 2024)、ABC (Kolawole et al., 2025))と比較評価したで。数学的推論(GSM8K、CNK12)とコード生成(HumanEval、MBPP)のベンチマークでな。リアクティブ・シェパーディングは全データセットで精度あたりコスト効率(ACE)が一番高くて、難しい多言語クエリ(CNK12)ではルーティングのベースラインより2倍もコスト削減できたで。
---
図2. SLM(Llama-3.2-3B-Instruct)の正解率をLLM(Llama-3.3-70B-Versatile)のヒントサイズごとに見たグラフやで。ちっちゃいヒント(LLMフル回答の10〜30%くらい)でもめっちゃ正解率上がるんやけど、60%超えたあたりから効果は頭打ちになってくるねん。これがシェパーディングの動機やねん:LLMにフル回答もらうんやなくて、ヒントだけもらおうっていう発想や。破線は各データセットでのLLMの正解率を示してるで。
---
なんでかっていうと、LLMにフル回答作らせるんやなくて、シェパーディングはLLMに短い接頭辞だけ出力してもらうねん。LLM回答の最初のnトークンだけや。これを「ヒント」って呼んでるんや。で、このヒントをクエリとくっつけてSLMに渡して、最終回答を出してもらうわけやな。LLMのヒントがSLMの推論に役立つかどうか検証するために、数学的推論(GSM8K (Cobbe et al., 2021)とCNK12 (OpenR1, 2025))とコード生成(HumanEval (Chen, 2021)とMBPP (Austin et al., 2021))の4つの有名なベンチマークで評価したで。SLMにはLlama-3.2-3B-Instruct、LLMにはLlama-3.3-70B-Versatile使ったで(Dubey et al., 2024)。図2見てもらったらわかるけど、ちょっとしたヒントでも全データセットでSLMの正解率がめっちゃ上がるんや。
図1に示してるように、シェパーディングには2つのモードがあるねん:1) **プロアクティブ・シェパーディング**(図1a)はルーティングベースのシェパーディングで、学習済みルーターがヒントが必要かどうかと何トークン要求するかを直接予測するんや。2) **リアクティブ・シェパーディング**(図1b)はカスケーディングベースのシェパーディングで、SLMの回答の特徴を使ってカスケーディングの判断とヒント予測をするんや。ちなみにプロアクティブ・シェパーディングは両極端にしたらルーティングと同じになるで:ヒントサイズゼロ(SLMだけ)か極大(LLMフル回答)やな。
---
## Page 3
[](/attach/4f91145b287ae51d50fb00db9c73a1abd8c4abfaa816d614e134c6b64fbc173e_p003.png)
### 和訳
LLM Shepherding(LLMの羊飼い方式)
クロスドメイン転送(HumanEval)において、カスケードベースラインと比べて2.8倍ものコスト削減を達成してんねん。しかも後者はコード特化の学習なしでこの結果やで(セクション4参照)。
## 2. 問題の定式化
### 2.1. システムと記法
まずQっていうのは全部のクエリ(問い合わせ)の集合で、q ∈ Qが個々のクエリを表してんねん。Xは有限のトークン(単語みたいなもん)の語彙で、X*はXから作れる全ての有限トークン列の集合やな。
ほんで、2つの言語モデルを考えるねん。1つ目はオープンソースのSLM(小さい言語モデル)hs : Q → X*で、これはスマホとかラップトップとかローカルサーバーみたいな手元のデバイスで動かすやつ。2つ目はLLM(大きい言語モデル)hl : Q → X*で、こっちはLLMのAPIを通じてアクセスするやつやねん。
任意のトークン列x ∈ X*について、|x|はそのサイズ(トークンの数)を表すで。2つの列x, y ∈ X*があったら、x ⊕ yでそれらをくっつけた(連結した)ものを表すねん。列xと整数n ≤ |x|があったら、x[1:n]でxの最初のn個のトークンからなる接頭辞を表すで。1[·]は標準的な指示関数やな。
品質関数ϕ : Q × X* → [0, 1]っていうのを定義するんやけど、これはクエリq ∈ Qに対する応答r ∈ X*の品質を測るもんやねん。値が高いほど応答の品質がええってことや。実際のところ、ϕは完全一致の正解率(正解がある問題用)やったり、意味的類似度スコアやったり、学習済みの報酬モデルやったりするで。品質閾値τ ∈ (0, 1]を定義して、Is(q) = 1[ϕ(q,hs(q))≥τ]でSLMだけで満足できる応答が出せるかどうかを示すねん。
### 2.2. ヒントとShepherdingポリシー
LLM shepherdingの中心的な概念は「ヒント」やねん。これはLLMの応答の接頭辞(先頭部分)をSLMに渡して、生成をガイドするもんやで。数式で書くと、クエリqとヒントサイズn ≥ 0に対して、ヒントはこう定義されるねん:
hint(q, n) = hl(q)[1:n]
ほんで、ヒント付きのSLM応答はこうなるで:
h(n)_s(q) = hs(q ⊕ hint(q, n))
つまりSLMは、元のクエリにヒント接頭辞をくっつけたものを条件として応答を生成するわけやな。
**Shepherdingポリシー**:shepherdingポリシーπ : Q → {0, 1, ..., Nmax}は、各クエリqをヒントサイズn = π(q)に対応させるもんやねん。NmaxはLLMの最大出力トークン数やで。n = 0のときはSLMが助けなしで応答して、n > 0のときはSLMが完成させる前にnトークンのヒントをリクエストするってことやな。
各クエリqに対して、最小ヒントサイズっていうのを定義するんやけど、これはSLMが満足できる応答を出すのに必要なLLMトークンの最小数のことやで:
n*(q) = min{n ∈ Z≥0 : ϕ(q, h(n)_s(q)) ≥ τ} (1)
**Oracleシェパディングポリシー**π*は、各クエリqをn*(q)に対応させるもんやねん。
### 2.3. コストモデルと評価指標
商用LLM APIの料金に合わせた、トークンベースのコストモデルを採用してるで。cin_lとcout_lをそれぞれLLMの入力トークン単価と出力トークン単価としようや。同様に、cin_sとcout_sをSLMの対応するコストとするで。ローカルデバイスにデプロイしたオープンソースSLMの場合、cin_s = cout_s = 0やねん。
ヒントサイズn > 0でクエリqをshepherdingするコストはこうなるで:
cshep(q, n) = |q|cin_l + ncout_l + (|q| + n)cin_s + |h(n)_s(q)|cout_s
異なる戦略やポリシー間のコストパフォーマンスのトレードオフを比較するために、Accuracy-per-Cost Efficiency(ACE、正解率あたりのコスト効率)っていう正規化された効率指標を導入するで。Alをリモートの大規模モデルの正解率として、その総コストをCl = Σq∈Q cl(q)とするやん。Asをオンデバイスの小規模モデルの正解率として、そのコストはゼロ(cin_s = cout_s = 0と仮定)やな。
ポリシーπの正解率がAπで総コストがCπのとき、Accuracy-Cost Efficiencyをこう定義するで:
ACE(π) = [(Aπ - As)/(Al - As)] / [Cπ/Cl]
これはSLMとLLMのベースラインに対する、コスト単位あたりの正解率向上を捉えてんねん。ちなみにACE計算からはSLM単独ポリシーは除外してるで。なんでかっていうと、SLMだけで十分な能力があるシナリオやったら、shepherdingとかSLM-LLM協調フレームワーク自体が意味なくなるからやねん。
戦略間の公平な比較のために、目標品質レベルを保証しながら達成できる最小コストも示してるで。これは次の問題として定式化されるねん。
**問題**:クエリ分布Dと目標期待品質τが与えられたとき、品質目標を達成しながら期待コストを最小化するポリシーπ*を見つけよ:
min_π E[cshep(q, π(q))]
制約条件:E[ϕ(q, h(π(q))_s(q))] ≥ τ (2)
### 2.4. コスト分析(Oracle)
Oracle(最適な)意思決定の下での、ルーティング、カスケーディング、shepherdingの金銭的コストを分析するで。ルーティングはSLMの全コスト(SLMが
---
## Page 4
[](/attach/4f91145b287ae51d50fb00db9c73a1abd8c4abfaa816d614e134c6b64fbc173e_p004.png)
### 和訳
LLM シェパーディング(羊飼い方式)
(ヒントだけで済むか、エスカレーションが必要でフルのLLMコストがかかるか、どっちかやねん。両方払うことはないで。カスケーディング方式やと、まずSLM(小さいモデル)のコストが絶対かかって、そのSLMが失敗したら追加でフルのLLMコストもかかるから、結局両方のモデル分払わなあかんこともあるわけや。シェパーディング方式やと、ヒントいらん時(n*(q)=0の時)はSLMのコストだけで済むし、ヒントが必要な時でも、(i)クエリ処理のLLM入力コスト、(ii)n*(q)トークン分のヒント生成のLLM出力コスト、(iii)ヒント付きの入力を処理するSLMコスト、これだけやねん。ほんで、こういう命題が成り立つわけや。
**命題 2.1(オラクルコスト)** オラクル(神様みたいに最適な判断ができる状態)での意思決定において、クエリq∈Qごとの金銭コストは、ルーティング、カスケーディング、シェパーディングそれぞれでこうなるで:
[数式はそのまま]
ここで h(n)_s(q) = h_s(q ⊕ hint(q, n)) っていうのは、nトークンのヒントで補強された時のSLMの応答のことやで。
オープンソースのSLMを自分のデバイスとかプライベートのインフラで動かす場合は、c^in_s = c^out_s = 0 になるねん。この仮定のもとやと、次の系が成り立つで(証明は付録Aにあるわ)。
**系 2.2** もし c^in_s = c^out_s = 0 やったら、全てのクエリ q ∈ Q について:
c*_shep(q) ≤ c*_route(q) = c*_casc(q)
シェパーディングのコスト優位性はな、LLMのフル出力コスト |h_l(q)|c^out_l を、部分的なヒントコスト n*(q)c^out_l に置き換えられるところから来てるねん。LLMの出力トークンって普通は一番コストかかる部分やねん(商用APIのほとんどで c^out_l > c^in_l やし)、やから出力トークン数をちょっと減らすだけでもめっちゃ節約になるわけや。
**注釈 2.3** 命題2.1と系2.2のコスト式は、プロアクティブ(先回り型)シェパーディングにそのまま適用できるで。リアクティブ(後追い型)シェパーディングやと追加でSLM推論コストがかかるんやけど、c^in_s = c^out_s = 0 の時はオラクルコストは同じになって、系2.2は両方のパターンで成り立つねん。
## 3. シェパーディングシステムの学習
目標はな、最小ヒントサイズ n*(q) を予測するポリシー π_θ: Q → Z_≥0 を学習することやねん。でもな、n*(q) を直接予測するんはいくつかの理由でめっちゃ難しいねん:
1) **ヒントサイズの分布が偏りまくり**:n*(q) はクエリによってめっちゃバラつくねん。GSM8Kやと、80.6%のクエリはヒントいらんのに、残りの19.4%はLLMの完全な応答の10%から90%まで幅広く分布してるねん(詳しい議論は付録Dを見てな)
2) **効果が急に変わる**:nをちょっと変えただけで、SLMが品質閾値τを超えるかどうかがガラッと変わることあるねん。重要な情報(キーとなる制約とか中間ステップとか)が特定のトークン境界に現れることあるからな
3) **品質が単調やない**:品質関数 ϕ(q, h^(n)_s(q)) は n に対して単調増加するとは限らんねん(図2見てな)。ヒントトークンが多すぎるとSLMを縛りすぎて、短いヒントやったら成功してたのに、かえって性能落ちることあるねん
4) **トークン化に敏感**:同じ意味の内容でも、モデルやクエリの言い回しによってトークン数変わるから、絶対的なトークン数への直接回帰はもろいねん
これらの課題に対処するために、2段階のポリシー設計を採用したで:まずヒントが必要かどうか(つまり n*(q) > 0 かどうか)を予測して、ヒントが必要な場合にのみ、必要なヒントサイズを予測するねん。具体的には、二値分類器 y(q) = 1[n*(q)>0] と、n*(q) > 0 のクエリのサブセットに対する n*(q) の回帰モデルを学習するで。
### 3.1 学習データと教師信号
シェパーディングモデルを学習するために、離散化されたヒントサイズで候補ヒントを評価して、教師ラベル n*(q) を構築するねん。各クエリ q について、LLMの完全な応答長 |h_l(q)| に対するパーセンテージ p ∈ {0, 10, 20, ..., 90} でヒントを生成するねん。n_p = ⌊(p/100)|h_l(q)|⌋ を計算して、max_new_tokens = n_p でLLMにクエリして hint(q, n_p) = h^(n_p)_l(q) を取得するわけや。ほんで各ヒントを評価するために、ヒント付きプロンプトでSLMを実行して、最小十分サイズを記録するねん:
n*(q) = min {n_p : ϕ(q, h_s(q ⊕ hint(q, n_p))) ≥ τ}
どの部分ヒントも閾値を満たさへん場合は、n*(q) = |h_l(q)| に設定してLLMの完全な応答を使うで。ラベリング手順、離散化の粒度、設計の理由についての詳しい議論は付録B.1にあるわ。どのヒントサイズでもSLMの精度が改善せえへんし、LLMの応答も間違ってるサンプルはフィルタリングするで。詳細は付録Cを見てな。
y(q) = 1[n*(q)>0] やったな。ヒントが必要なクエリに対する対数変換されたヒントサイズは r(q) = log(1 + n*(q)) やで。モデルはヒント要/不要分類用のロジット ŷ(q) とヒントサイズの予測 r̂(q) を出力するねん。
### 3.2 モデルアーキテクチャ
テキストエンコーダーとして DeBERTa-v3-large(He et al., 2023)を使うで。h_CLS(q) をクエリ q の [CLS] 埋め込みとするわ。f(q) を入力特徴ベクトルとするで。これを多層パーセプトロン(MLP)に通して、変換された数値特徴 g(q) = MLP(f(q)) を得るねん。融合表現 u(q) = [h_CLS(q); g(q)] を構築するで。この u(q) を使って、シェパーディングシステムは以下を出力するねん:
ŷ(q) = Head_hint(u(q)) ∈ R
---
## Page 5
[](/attach/4f91145b287ae51d50fb00db9c73a1abd8c4abfaa816d614e134c6b64fbc173e_p005.png)
### 和訳
# LLMシェパーディング
$\hat{r}(q) = \text{Headsize}(u(q)) \in \mathbb{R}$
ここで$\hat{y}(q)$はヒント指標$y(q)$に対するロジットで、$\hat{r}(q)$は$r(q)$を予測するもんやねん。$\text{Headhint}$と$\text{Headsize}$は軽量な予測ヘッド(ちっちゃいフィードフォワードネットワークやな)で、共有された融合表現$u(q)$にくっついとるんよ。$\text{Headhint}$は$u(q)$を1個のスカラーロジットに変換して二値分類(ヒント必要 vs ヒント不要)をするし、$\text{Headsize}$は$u(q)$を回帰ターゲット$r(q)$用の1個のスカラーに変換するわけや。ヒント指標ロジットの分散を抑えるために、マルチサンプルドロップアウトを適用して、複数パスのロジットを平均化しとるで(Inoue, 2019)。
## 3.3. 学習目的
ヒントが必要なクエリ($\pi_\theta(q) > 0$のやつ)に対しては、低複雑度と高複雑度のクエリをさらに区別するためにヒントサイズ閾値$\eta_{\text{hint}}$を導入するんや:
- $0 < \pi_\theta(q) \leq \eta_{\text{hint}}$の場合:max_new_tokens = $\pi_\theta(q)$に設定してLLMにヒントを問い合わせて、$\text{hint}(q, \pi_\theta(q)) = h_l^{(\pi_\theta(q))}(q)$を取得し、シェパーディングされた応答$h_s(q \oplus \text{hint}(q, \pi_\theta(q)))$を返すで
- $\pi_\theta(q) > \eta_{\text{hint}}$の場合:そのクエリは高複雑度やと判断されてLLMに直接ルーティングされ、SLMを呼び出さずに$h_l(q)$を返すんや
学習セット全体で同時最適化するねん。ヒント指標には、ロジット$\hat{y}(q)$に対するバイナリクロスエントロピーを使うで:
$$L_{\text{hint}} = -\left[ y(q) \log \sigma(\hat{y}(q)) + (1 - y(q)) \log(1 - \sigma(\hat{y}(q))) \right]$$
クラス不均衡にはミニバッチバランシングで対応しとるわ。
ヒントサイズについては、正例のみ$Q^+ = \{q \in Q | y(q) = 1\}$でSmooth L1(Huber)損失(Huber, 1964)を使って学習するねん:
$$L_{\text{size}} = \frac{1}{|Q^+|} \sum_{q \in Q^+} \text{SmoothL1}(\hat{r}(q) - r(q))$$
これは対数変換されたターゲットの回帰残差にペナルティを与えるんやけど、$\ell_2$損失よりも外れ値に強いんよ。直感的に言うと、$L_{\text{size}}$はヒントが必要な時($y(q) = 1$)だけ計算されるわけや。なんでかっていうと、ヒント不要のクエリにはサイズの定義がないからやねん。
総合損失は$L = \lambda L_{\text{hint}} + (1-\lambda) L_{\text{size}}$で、$\lambda \in [0, 1]$は相対重みパラメータやで。AdamWの使用、EMA、重み付きサンプリングによるクラスバランシング、ポリシーキャリブレーション手順など、追加の最適化詳細は付録B.2に載っとるわ。
## 3.4. 推論:予測から決定へのマッピング
テスト時には、まず二値分類ヘッドからヒント確率を計算するで:$P(q) = \sigma(\hat{y}(q))$、ここで$\sigma(\cdot)$はシグモイド関数やねん。ほんでから閾値$\alpha \in [0, 1]$を使って二値ヒント決定$\mathbf{1}_{[P(q) \geq \alpha]}$を得るんや。予測ヒントサイズは次のように定義されるで:
$$\pi_\theta(q) = \begin{cases} 0, & \text{if } P(q) < \alpha \\ \lfloor \text{clip}(\exp(\hat{r}(q)) - 1, 0, N_{\max}) \rceil, & \text{if } P(q) \geq \alpha \end{cases}$$
ここで$\lfloor x \rceil$は$x$を最も近い整数に丸めることを表し、$\text{clip}(x, a, b) = \max(a, \min(x, b))$は値を区間$[a, b]$に制限するんや。$N_{\max}$はLLMの最大出力トークン制限やで。パラメータ$\theta$は学習されたモデルコンポーネント全部(バックボーンエンコーダ、MLP、予測ヘッド)を含んどるわ。
**ヒント閾値について。** ヒント不要のクエリ($\pi_\theta(q) = 0$)には、SLMの直接出力$h_s(q)$を返すねん。ヒントが必要なクエリ($\pi_\theta(q) > 0$)には、さらにヒントサイズ閾値$\eta_{\text{hint}}$を導入して低複雑度と高複雑度のクエリを区別するんや。
この閾値ベースのルーティングは、めっちゃ長いヒントが必要なクエリはLLMのフル推論能力で直接処理した方がええかもしれんっていう直感を捉えとるねん。長いヒントを生成するオーバーヘッドをかけた挙句、結局SLMを呼び出すのは避けたいやろ?閾値$\eta_{\text{hint}}$はコストと精度のバランスを取るために検証セットでチューニングするハイパーパラメータやで。
## 3.5. リアクティブシェパーディング:カスケード決定
ここまでは、プロアクティブシェパーディングで使うシェパーディングモデルについて説明してきたで。リアクティブシェパーディングでは、シェパーディングモデルの前にカスケード決定モジュールを追加するんや。さらに、SLMの応答からの特徴量もシェパーディングモデルの学習に組み込むで。
カスケード決定はSLMの応答間の一致に基づいて行うねん。これは学習不要のシンプルな手法で、効果的やって実証されとる(Kolawole et al., 2025)。具体的には、各クエリに対してSLMを温度サンプリング($T = 0.3$)で$K$回独立に実行して、候補回答$\{A_1, \ldots, A_K\}$と関連する予測エントロピー$\{e_1, \ldots, e_K\}$を生成するんや。決定論的デコーディングやなくて確率的サンプリングを使うのは、応答の多様性を得るためで、それによってSLMの認識論的不確実性を応答のばらつきと予測エントロピーから測定できるわけや。実験では$K = 3$に設定しとるで。シグナル品質と計算コストの実用的なバランスやねん。数学とコーディングのデータセットを扱っとるから、応答間の一致は最終回答の完全一致に基づいとるわ。$K$個中少なくとも$k$個の回答が一致したら、一致したSLM回答を直接出力するで。そうでなければ、シェパーディングモデルを呼び出すんや。
$k$の選択は精度とコストのトレードオフを反映しとるねん:$k = 3$(全員一致)はより保守的で、偽陰性を減らす代わりにルーティング率とLLMコストが高くなるわ。一方$k = 2$(多数決)はより積極的で、より多くのクエリがLLMをバイパスできるけど、SLMの直接出力でエラーが増えるリスクがあるんや。両方の設定を実験で検証しとるで(セクション4)。
SLMから複数の応答が得られたら、以下の特徴量を計算してシェパーディングモデルの学習に組み込むんや。
---
## Page 6
[](/attach/4f91145b287ae51d50fb00db9c73a1abd8c4abfaa816d614e134c6b64fbc173e_p006.png)
### 和訳
ほな、この論文の内容を説明していくで!
**・平均エントロピー**: ¯e(q) = 1/K × Σei やねん。これはな、モデルが全体的にどんだけ「わからへん」って思ってるかを数値化したもんや。
データは訓練用に18,251個、検証用に1,073個、テスト用に2,147個に分けてあるで。
**LLMシェパーディング(羊飼い方式)**
**・平均出力長**: ¯Lout(q) = 1/K × Σ|Ai| や。これは普通の回答がどんだけ複雑かを表してるねん。
**・クエリの長さ**: |q| で、バックボーンモデルのトークナイザーでトークン数として測るんや。
なんでかっていうと、文字数じゃなくてトークン数で長さを見るのは、トークン化がモデルの内部表現とピッタリ合ってて、推論の複雑さをもっと意味のある形で捉えられるからやねん。長い出力って普通、何段階も考えなあかん解答やから、途中の推論ステップが多いってことや。トークンベースの特徴量なら、推論時に余計なトークン化処理いらんから、効率的にまとめて処理できるってわけ。
これらの特徴量は標準化されて、軽量なMLPでテキスト表現と組み合わせるんや。イメージ的には、エントロピーが高いほど小さいモデル(SLM)の回答が不安定やってことで、「ヒントあげた方がええで」ってサインになるねん。出力長の統計は、そのクエリにどんだけ詳しく答えなあかんかの追加情報を教えてくれるんや。
**4. 性能比較**
このセクションでは、プロアクティブ(先回り型)とリアクティブ(後追い型)のシェパーディング戦略のコストと精度を、最新のLLMルーティングやカスケード戦略と比べてみたで。ルーティングのベースラインはRouteLLMとGraphRouter、カスケードのベースラインはFrugalGPTとABCを使ったんや。SLMには素のLlama-3.2-3B-Instruct(ファインチューニングなし)を使って、NVIDIA RTX 5090 GPUを積んだローカルサーバーで動かしたで。LLMの方は、Groq API経由でLlama-3.3-70B-Versatileに問い合わせてて、入力100万トークンあたり$0.59、出力100万トークンあたり$0.79やねん。
**4.1. データセットと実験設定**
**データセット**:数学的推論とコード生成の4つのベンチマークで全手法を評価したで。
**(a) GSM8K**:小学校レベルの算数データセットで、訓練用7,473問、テスト用1,319問あるねん。テストに776問、検証に残りの543問を使ったわ。各問題は何段階かの計算が必要で、自然言語の解説と数値の答えがセットになってるんや。
**(b) CNK12**:中国のK-12(小中高)数学ベンチマークで、OpenR1-Math-220kデータセットから作ったもんや。代数、幾何、微積分とか、小学校から高校までいろんな分野をカバーしてるねん。全データセットから21,471問をランダムに抜き出して、訓練用18,251問、検証用1,073問、テスト用2,147問に分けたで。
**(c) HumanEval**:コード生成ベンチマークで、164個のプログラミング問題があるねん。各問題には関数シグネチャ、docstring、本体、それと検証用の複数のユニットテストが含まれてるんや。このベンチマークは、GSM8Kで訓練したモデルをコード専用の訓練なしで評価して、うちのアプローチの汎化能力を見せつけたったで。
**(d) MBPP**:Mostly Basic Python Problemsベンチマークで、クラウドソーシングで集めた入門レベルのプログラミング課題が974個あるねん。各課題に解答検証用の自動テストケースが3つずつついてるわ。MBPPはゼロショット、つまりデータセット固有の調整なしで評価したで。
**推論と評価**:テストセットには事前計算されたヒントは入ってへんで。推論時には、うちのポリシーがヒントサイズπθ(q)を予測するねん。ヒントが必要やったら、max_new_tokensをπθ(q)に設定してLLMに問い合わせて、途中で切った接頭辞を元のプロンプトに追加してSLMに続きを書かせるんや。全部の生成でtemperature 0.3、top-p 0.95を使ってるで。詳しいプロンプトテンプレートは付録Eに載せてあるわ。
数学ベンチマーク(GSM8K、CNK12)では、最終的な数値の答えを抜き出して正解と比べるねん。コーディングベンチマーク(HumanEval、MBPP)では、生成されたコードを実行して全ユニットテストが通るか確認するんや。サンプリングのばらつきがあっても信頼できる精度を出すために、各クエリで7回独立して試行して多数決で決めたで。
**4.2. 性能分析**
表1〜4に4つのベンチマークの結果をまとめてあるで。ベースラインのルーティングとカスケード戦略には、著者がGitHubで公開してるデフォルトのパラメータ設定を使ったわ。プロアクティブとリアクティブのシェパーディングのηhint、α、Kの値は付録Fに載せてあるで。見てみ、リアクティブシェパーディングが全データセットで最高のACEを叩き出してて、1.25(CNK12)から2.78(MBPP)の範囲やねん。しかもLLMだけ使う場合と比べてコストを42〜94%も削減しとるんや。
**ルーティングとの比較**:ルーティングのベースライン(RouteLLM、GraphRouter)は、クエリの難易度がめっちゃバラバラやと苦戦するねん。CNK12では、LLMと比べてたった5〜8%しかコスト削減できへんかったけど、リアクティブシェパーディングは42%削減したんや。同じくらいの精度で2倍の改善やで!GSM8Kやと差は小さいねんけど、これは大半のクエリがSLMで解けるからや。それでもシェパーディングはOracle(理想的な性能)と同じ$0.034を達成してて、ルーティング手法は2〜3倍高いコストがかかってしもてるんや。
**カスケードとの比較**:カスケードのベースライン(FrugalGPT、ABC)はルーティングより高い精度を出すけど、その分コストも高くなるねん。GSM8Kでは、ABCが94.9%の精度を達成して...
---
## Page 7
[](/attach/4f91145b287ae51d50fb00db9c73a1abd8c4abfaa816d614e134c6b64fbc173e_p007.png)
### 和訳
LLM Shepherding
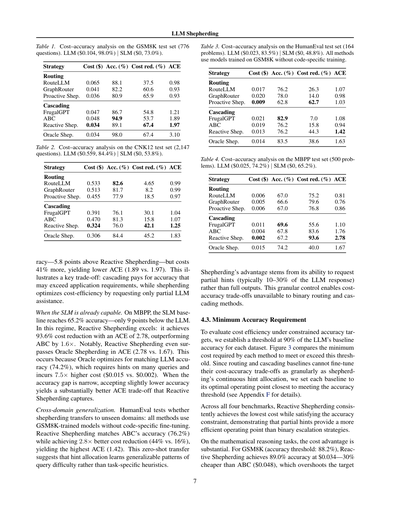
表1. GSM8Kテストセット(776問)のコストと精度の分析やで。LLMは($0.104で、98.0%の精度)、SLMは($0で、73.0%の精度)やねん。
表3. HumanEvalテストセット(164問)のコストと精度の分析や。LLMは($0.023で、83.5%の精度)、SLMは($0で、48.8%の精度)やで。全部の手法はGSM8Kで学習したモデルを使ってて、コード専用の学習はしてへんねん。
| 戦略 | コスト ($) | 精度 (%) | コスト削減 (%) | ACE |
|------|-----------|---------|--------------|-----|
| **ルーティング** |
| RouteLLM | 0.065 | 88.1 | 37.5 | 0.98 |
| GraphRouter | 0.041 | 82.2 | 60.6 | 0.93 |
| Proactive Shep. | 0.036 | 80.9 | 65.9 | 0.93 |
| **カスケーディング** |
| FrugalGPT | 0.047 | 86.7 | 54.8 | 1.21 |
| ABC | 0.048 | 94.9 | 53.7 | 1.89 |
| Reactive Shep. | 0.034 | 89.1 | 67.4 | 1.97 |
| Oracle Shep. | 0.034 | 98.0 | 67.4 | 3.10 |
表2. CNK12テストセット(2,147問)のコストと精度の分析やねん。LLMは($0.559で、84.4%の精度)、SLMは($0で、53.8%の精度)や。
| 戦略 | コスト ($) | 精度 (%) | コスト削減 (%) | ACE |
|------|-----------|---------|--------------|-----|
| **ルーティング** |
| RouteLLM | 0.533 | 82.6 | 4.65 | 0.99 |
| GraphRouter | 0.513 | 81.7 | 8.2 | 0.99 |
| Proactive Shep. | 0.455 | 77.9 | 18.5 | 0.97 |
| **カスケーディング** |
| FrugalGPT | 0.391 | 76.1 | 30.1 | 1.04 |
| ABC | 0.470 | 81.3 | 15.8 | 1.07 |
| Reactive Shep. | 0.324 | 76.0 | 42.1 | 1.25 |
| Oracle Shep. | 0.306 | 84.4 | 45.2 | 1.83 |
精度の話でいうと、ABCはReactive Shepherdingより5.8ポイント高いんやけど、コストが41%も余計にかかるから、ACEは低くなるねん(1.89対1.97)。ここがめっちゃ大事なトレードオフやねん。なんでかっていうと、カスケーディングはアプリケーションの要件を超えるかもしれん精度のために金払ってしまうけど、Shepherdingは部分的なLLMの助けだけを頼むことでコスト効率を最適化しとるからやねん。
**SLMがすでに優秀な場合**。MBPPでは、SLMのベースラインが65.2%の精度を達成しとって、LLMとの差はたった9ポイントやねん。この状況やとReactive Shepherdingがめっちゃ輝くで。93.6%のコスト削減とACE2.78を達成して、ABCの1.6倍の性能を出しとるねん。注目すべきは、Reactive ShepherdingがOracle ShepherdingのACEすら超えとることや(2.78対1.67)。なんでこうなるかっていうと、OracleはLLMの精度(74.2%)に合わせることを最適化するから、めっちゃ多くのクエリにヒントが必要になって、コストが7.5倍もかかるねん($0.015対$0.002)。精度の差が小さい時は、ちょっと低い精度を受け入れた方がめっちゃええACEのトレードオフになって、それをReactive Shepherdingはうまく捉えとるんやな。
**異なるドメインへの汎化性能**。HumanEvalはShepherdingが未知のドメインに転移できるかをテストしとるねん。全部の手法がGSM8Kで学習したモデルを使ってて、コード専用のファインチューニングはしてへんのや。Reactive ShepherdingはABCと同じ精度(76.2%)を達成しながら、コスト削減は2.8倍も良くて(44%対16%)、最高のACE(1.42)を叩き出しとるねん。このゼロショット転移から分かることは、ヒント割り当ては特定のタスクに特化したヒューリスティックやなくて、クエリの難しさの汎用的なパターンを学習しとるってことやな。
表3.(再掲)HumanEvalテストセットのコストと精度の分析。
| 戦略 | コスト ($) | 精度 (%) | コスト削減 (%) | ACE |
|------|-----------|---------|--------------|-----|
| **ルーティング** |
| RouteLLM | 0.017 | 76.2 | 26.3 | 1.07 |
| GraphRouter | 0.020 | 78.0 | 14.0 | 0.98 |
| Proactive Shep. | 0.009 | 62.8 | 62.7 | 1.03 |
| **カスケーディング** |
| FrugalGPT | 0.021 | 82.9 | 7.0 | 1.08 |
| ABC | 0.019 | 76.2 | 15.8 | 0.94 |
| Reactive Shep. | 0.013 | 76.2 | 44.3 | 1.42 |
| Oracle Shep. | 0.014 | 83.5 | 38.6 | 1.63 |
表4. MBPPテストセット(500問)のコストと精度の分析やで。LLMは($0.025で、74.2%の精度)、SLMは($0で、65.2%の精度)やねん。
| 戦略 | コスト ($) | 精度 (%) | コスト削減 (%) | ACE |
|------|-----------|---------|--------------|-----|
| **ルーティング** |
| RouteLLM | 0.006 | 67.0 | 75.2 | 0.81 |
| GraphRouter | 0.005 | 66.6 | 79.6 | 0.76 |
| Proactive Shep. | 0.006 | 67.0 | 76.8 | 0.86 |
| **カスケーディング** |
| FrugalGPT | 0.011 | 69.6 | 55.6 | 1.10 |
| ABC | 0.004 | 67.8 | 83.6 | 1.76 |
| Reactive Shep. | 0.002 | 67.2 | 93.6 | 2.78 |
| Oracle Shep. | 0.015 | 74.2 | 40.0 | 1.67 |
Shepherdingの強みは、完全な出力やなくて部分的なヒント(だいたいLLMの回答の10〜30%くらい)を要求できることやねん。この細かいコントロールがあるから、二者択一のルーティングやカスケーディングでは実現できひんコストと精度のトレードオフができるんやな。
**4.3. 最低精度要件**
精度の制約がある条件下でのコスト効率を評価するために、各データセットでLLMのベースライン精度の90%を閾値として設定したんや。図3は、この閾値を満たすか超えるために各手法が必要とする最小コストを比較しとるねん。ルーティングとカスケーディングのベースラインは、Shepherdingの連続的なヒント割り当てほど細かくコストと精度のトレードオフを調整できひんから、各ベースラインは精度閾値を満たすのに最も近い最適な動作点に設定しとるで(詳細は付録Fを見てな)。
4つ全部のベンチマークで、Reactive Shepherdingは精度制約を満たしながら一貫して最低コストを達成しとって、部分的なヒントは二者択一のエスカレーション戦略よりも効率的な動作点を提供するってことを示しとるねん。
数学的推論タスクでは、コストの優位性がめっちゃ大きいで。GSM8K(精度閾値:88.2%)では、Reactive Shepherdingは89.0%の精度を$0.034で達成しとって、目標を超過するABC($0.048)より30%も安いねん。
---
## Page 8
[](/attach/4f91145b287ae51d50fb00db9c73a1abd8c4abfaa816d614e134c6b64fbc173e_p008.png)
### 和訳
**LLMシェパーディング**
プロアクティブ・シェパーディングっていうのはな、小さいモデル(SLM)が動く**前に**ヒントを出すかどうか決めるねん。せやから遅延がほとんど増えへんのよ。一方でリアクティブ・シェパーディングは、まずSLMに3回答えさせて合意形成とか特徴ベクトル作成をするねん(1,163.48ミリ秒かかる)、その後で判断モジュールを呼び出す(7.32ミリ秒)—これ全体の0.6%しかオーバーヘッドないねん。つまりな、リアクティブの方がコストと精度のバランスはめっちゃええんやけど、プロアクティブの判断処理はローカルサーバーで159倍も速いってわけや。
**5. 研究の範囲と今後の方向性**
この研究はな、数学の問題解いたりコード書いたりする「答え合わせできるタスク」に絞ってるねん。正解かどうか自動でチェックできるやつな。要約とか創作みたいな正解が一つに決まらへんタスクに応用するなら、「正解/不正解」の二択判定じゃなくて、学習済みの報酬モデルとか人間の評価に置き換えなあかん。これは今後の課題として残してるで。
実験では同じモデルファミリーのSLMとLLMペア(Llama 3.2と3.3)使ってんねん。トークナイザーが共通やからな。ほんで気になるのは、SLMとLLMで違うトークナイザーとかアーキテクチャ使ったらどうなるん?っていう話や。例えばMixtralとかQwenとかな。ヒントのプレフィックスがモデル間で意味的にズレる可能性あるやろ。
**6. 結論**
俺らはな、今まで主流やった「ルーティングとカスケード」っていう二者択一の考え方に一石を投じたったわけや。あれはLLMを「使うか使わへんか」のオール・オア・ナッシングで扱ってたやろ。でもLLMシェパーディングを導入することで、ほんまに効率ええ高品質推論への道は、**モデルを選ぶことちゃうねん、ターゲット絞った協力させることやねん**って証明したったわ。この仕組みはトークン単位で予算コントロールして、フロンティアLLMから短いヒント(プレフィックス)だけもらって、SLMの精度上げるんや。
俺らの発見で、LLMシェパーディングがコスト効率ええ運用の新しいアプローチやって確立されたな。リアクティブ・シェパーディングは全ベンチマークで**精度あたりコスト効率(ACE)が最高**やねん。LLMだけ使う場合と比べて42〜94%もコスト削減できて、ルーティングベースラインより2倍、カスケードベースラインより2.8倍もコスト削減効果がええんや(精度は同等で)。適応型ヒント配分メカニズムは汎化性能もすごいで:数学データセットだけで学習させたのに、コード生成にゼロショットで転移できて、HumanEvalでカスケードと同じ精度をコストの一部で達成してる。MBPPでは、リアクティブ・シェパーディングがなんと**オラクル・シェパーディングをACEで超えてる**ねん。これが何を意味するかっていうと、SLMがそもそも能力あるときは、部分的なヒントの方がLLMにフルで任せるより効くってことや。
**(a) 数学データセット**
**(b) コーディングデータセット**
**図3.** 各データセットでLLM精度の90%を達成するための最小コスト。各手法は最適な動作点にチューニングされてて、精度要件を満たすか超えてる(棒グラフの上に表示)。
94.8%の精度で、必要以上の精度にお金払ってるわけや。FrugalGPT($0.049、88.7%)は閾値クリアしてるけど45%もコスト高い。これはな、信頼度ベースのエスカレーションがLLMフルコールを積極的にトリガーしすぎてるってことや。CNK12(閾値:76.0%)でも同じパターンやな:リアクティブ・シェパーディングは$0.324でターゲット達成、ABCとFrugalGPTはそれぞれ45%と21%コスト高いわ。
この優位性はコード生成データセットでもっと顕著になるで。HumanEval(閾値:75.2%)では、リアクティブ・シェパーディングのコストは$0.013で、ABCより34%、RouteLLMより24%安い。MBPPが一番差がはっきりしてて:$0.002で、次に安い手法(ABC、$0.004)より61%も安いねん。これはな、コード補完タスクは部分的なヒントが提供する「足場」からめっちゃ恩恵受けるってことやと思うわ。
結論としてな、精度要件が固定されてる場合—本番環境のSLA(サービスレベル契約)ではよくあるシナリオやけど—適応型ヒント配分が優れたコスト効率を実現するってことや。
**4.4. レイテンシのオーバーヘッド:プロアクティブ vs リアクティブ**
CNK12でNVIDIA RTX 5090 GPUを使って、Llama-3.2-3B-Instructの推論レイテンシを測ったで。シェパーディングポリシーの追加はクエリあたりたった7.32ミリ秒—SLMの生成時間(1回あたり384.62ミリ秒)と比べたら無視できるレベルやな。
---
## Page 9
[](/attach/4f91145b287ae51d50fb00db9c73a1abd8c4abfaa816d614e134c6b64fbc173e_p009.png)
### 和訳
LLM シェパーディング
参考文献
Aggarwal, P., Madaan, A., Anand, A., Potharaju, S. P., Mishra, S., Zhou, P., Gupta, A., Rajagopal, D., Kappaganthu, K., Yang, Y., ほか。Automix: 言語モデルを自動でミックスする方法やねん。Proc. NeurIPS, 37:131000–131034, 2024年。
Austin, J., Odena, A., Nye, M., Bosma, M., Michalewski, H., Dohan, D., Jiang, E., Cai, C., Terry, M., Le, Q., and Sutton, C. 大規模言語モデルでプログラム合成するって話やで、2021年。
Behera, A. P., Champati, J. P., Morabito, R., Tarkoma, S., and Gross, J. 複数LLMを効率よく推論させるには?ルーティングとか階層的な手法の特徴と分析やねん。arXiv preprint arXiv:2506.06579, 2025年。
Cai, T., Li, Y., Geng, Z., Peng, H., Lee, J. D., Chen, D., and Dao, T. Medusa: 複数のデコーディングヘッド使ってLLMの推論をシンプルに加速させるフレームワークやで。arXiv preprint arXiv:2401.10774, 2024年。
Chen, C., Borgeaud, S., Irving, G., Lespiau, J.-B., Sifre, L., and Jumper, J. 投機的サンプリングで大規模言語モデルのデコーディングを加速する方法やねん、2023年。
Chen, G., Liao, M., Yu, P., Wang, D., Qiao, Z., Yang, C., Zhao, X., and Fan, K. C-3PO: 人間っぽい検索拡張生成を実現するためのコンパクトなプラグアンドプレイのプロキシ最適化やで、2025年。
Chen, L., Zaharia, M., and Zou, J. FrugalGPT: 大規模言語モデルをコスト抑えながら性能も上げて使う方法やねん。Transactions on Machine Learning Research, 2024年。ISSN 2835-8856。URL https://openreview.net/forum?id=cSimKw5p6R。注目の認定論文やで。
Chen, M. コードで訓練された大規模言語モデルの評価についてやねん。arXiv preprint arXiv:2107.03374, 2021年。
Cobbe, K., Kosaraju, V., Bavarian, M., Chen, M., Jun, H., Kaiser, L., Plappert, M., Tworek, J., Hilton, J., Nakano, R., Hesse, C., and Schulman, J. 数学の文章題を解くための検証器を訓練する話やで。arXiv preprint arXiv:2110.14168, 2021年。
Ding, D., Mallick, A., Wang, C., Sim, R., Mukherjee, S., Rühle, V., Lakshmanan, L. V. S., and Awadallah, A. H. ハイブリッドLLM: コスパ良くて質も担保するクエリルーティングやねん。Proc. ICLR, 2024年。
Dubey, A., Jauhri, A., Pandey, A., Kadian, A., Al-Dahle, A., Letman, A., Mathur, A., Schelten, A., Yang, A., Fan, A., ほか。Llama 3モデル群についての論文やで。2024年。
Feng, T., Shen, Y., and You, J. GraphRouter: LLM選択のためのグラフベースのルーターやねん。Yue, Y., Garg, A., Peng, N., Sha, F., and Yu, R. (編), Proc. ICLR, pp. 26186–26203, 2025年。
Gou, J., Yu, B., Maybank, S. J., and Tao, D. 知識蒸留についてのサーベイやで。International journal of computer vision, 129(6):1789–1819, 2021年。
Gu, Y., Dong, L., Wei, F., and Huang, M. MiniLLM: 大規模言語モデルの知識蒸留についてやねん。Proc. ICLR, 2024年。
Gupta, N., Narasimhan, H., Jitkrittum, W., Rawat, A. S., Menon, A. K., and Kumar, S. 言語モデルカスケード: トークンレベルの不確実性とその先の話やで。Proc. ICLR, 2024年。
He, P., Gao, J., and Chen, W. DeBERTav3: ELECTRA式の事前学習と勾配分離した埋め込み共有でDeBERTaを改良した話やねん、2023年。
Hinton, G., Vinyals, O., and Dean, J. ニューラルネットワークの中の知識を蒸留するってことやで。arXiv preprint arXiv:1503.02531, 2015年。
Hsieh, C.-Y., Li, C.-L., Yeh, C.-K., Nakhost, H., Fujii, Y., Ratner, A., Krishna, R., Lee, C.-Y., and Pfister, T. ステップバイステップで蒸留や!少ない訓練データと小さいモデルサイズでデカいモデルに勝つ方法やねん。Proc. ACL, pp. 8003–8017, 2023年。
Hu, Q. J., Bieker, J., Li, X., Jiang, N., Keigwin, B., Ranganath, G., Keutzer, K., and Upadhyay, S. K. RouterBench: 複数LLMルーティングシステムのベンチマークやで。arXiv preprint arXiv:2403.12031, 2024年。
Huber, P. J. 位置パラメータのロバスト推定についてやねん。The Annals of Mathematical Statistics, 35(1):73–101, 1964年。
Inoue, H. マルチサンプルドロップアウト: 訓練を加速して汎化性能も上げる方法やで。arXiv preprint, 2019年。
Jiang, D., Ren, X., and Lin, B. Y. LLM-Blender: ペアワイズランキングと生成的融合で大規模言語モデルをアンサンブルする話やねん。pp. 14165–14178, 2023年。
Kolawole, S., Dennis, D., Talwalkar, A., and Smith, V. 合意ベースのカスケーディングで効率的に推論する方法やで。TMLR, 2025年。ISSN 2835-8856。
Leviathan, Y., Kalman, M., and Matias, Y. 投機的デコーディングでTransformerの高速推論を実現するねん。Proc. ICML, pp. 19274–19286, 2023年。
Liu, X., Hu, L., Bailis, P., Cheung, A., Deng, Z., Stoica, I., and Zhang, H. オンライン投機的デコーディングについてやで。Proc. ICML, 2024年。
Loshchilov, I. and Hutter, F. 分離型重み減衰正則化の話やねん。Proc. ICLR, 2019年。
---
## Page 10
[](/attach/4f91145b287ae51d50fb00db9c73a1abd8c4abfaa816d614e134c6b64fbc173e_p010.png)
### 和訳
LLMシェパーディング(LLMの羊飼い的な誘導方法やな)
Lu, K., Yuan, H., Lin, R., Lin, J., Yuan, Z., Zhou, C., and Zhou, J. 「エキスパートにルーティングする:でっかい言語モデルを報酬ベースで効率よくアンサンブルする方法」 Proc. ACL, pp.1964–1974, 2024. ←これはな、複数のLLMがおる時に「このタスクはこいつが得意やから任せよ」って振り分けるやり方の研究やねん。
Morales-Brotons, D., Vogels, T., and Hendrikx, H. 「ディープラーニングにおける重みの指数移動平均:そのダイナミクスとメリット」 Transactions on Machine Learning Research, 2024. ISSN 2835-8856. ←モデルの重みを更新する時に、過去の値もちょっとずつ混ぜながら滑らかに更新していく手法やな。これやると学習が安定するねん。
Ong, I., Almahairi, A., Wu, V., Chiang, W.-L., Wu, T., Gonzalez, J. E., Kadous, M. W., and Stoica, I. 「RouteLLM:好みデータからLLMのルーティングを学習する」 Proc. ICLR, 2025. ←ユーザーの好みのデータを使って、どのLLMに仕事を振るか賢く判断するシステムやで。
OpenR1. 「Openr1-math-220k:数学の推論タスク用の大規模データセット」 2025. URL https://huggingface.co/datasets/open-r1/OpenR1-Math-220k. ←数学の問題解く能力を鍛えるための、めっちゃでかいデータセットやねん。
Subramanian, S., Elango, V., and Gungor, M. 「小さい言語モデル(SLMs)もまだまだパンチ力あるで:サーベイ論文」 arXiv preprint arXiv:2501.05465, 2025. ←でっかいモデルばっかり注目されがちやけど、小さいモデルでもちゃんと使えるでってことをまとめた論文やな。
Xu, M., Yin, W., Cai, D., Yi, R., Xu, D., Wang, Q., Wu, B., Zhao, Y., Yang, C., Wang, S., et al. 「リソース効率のええLLMとマルチモーダル基盤モデルのサーベイ」 arXiv preprint arXiv:2401.08092, 2024. ←計算資源をケチりながらも性能出すモデルについてまとめた論文やで。お金かかるからな、効率大事やねん。
Zhang, J., Wang, J., Li, H., Shou, L., Chen, K., Chen, G., and Mehrotra, S. 「Draft & Verify:自己投機的デコーディングによるロスレスなLLM高速化」 Proc. ACL, pp. 11263–11282, 2024. ←まず大雑把に下書き(ドラフト)を作って、それを検証するっていう二段階方式で、品質落とさずに推論を爆速にする手法やねん。めっちゃ賢いやろ。
10
---
## Page 11
[](/attach/4f91145b287ae51d50fb00db9c73a1abd8c4abfaa816d614e134c6b64fbc173e_p011.png)
### 和訳
A. 系2.2の証明
LLMシェパーディング
$c_{in}^s = c_{out}^s = 0$ を命題2.1に代入したら、こうなるねん:
route(q) = $(1 - I_s(q))(|q|c_{in}^l + |h_l(q)|c_{out}^l)$
casc(q) = $(1 - I_s(q))(|q|c_{in}^l + |h_l(q)|c_{out}^l)$
shep(q) = $|q|c_{in}^l + n^*(q)c_{out}^l$
ルーティングとカスケーディングって、小さいモデル(SLM)がタダで使える時は、オラクルコストが全く同じになるんよ。ほんで、シェパーディングとルーティング/カスケーディングを比べてみよか。
$I_s(q) = 1$ の時は $n^*(q) = 0$ になるから、3つの戦略全部コストゼロやねん。
$I_s(q) = 0$ の時はな、ルーティングとカスケーディングは $|q|c_{in}^l + |h_l(q)|c_{out}^l$ かかるんやけど、シェパーディングは $|q|c_{in}^l + n^*(q)c_{out}^l$ だけで済むねん。
定義上 $n^*(q) \leq |h_l(q)|$ やから、$c^*_{shep}(q) \leq c^*_{route}(q)$ ってことが言えるわけや。
B. シェパーディングシステムの学習:追加の詳細
B.1. 学習データセット構築の詳細
この付録では、シェパーディングモデルの教師あり学習に使う学習データセットの作り方を全部説明するで。離散化したトークン予算のアプローチとラベリング手順も含めてな。
離散化トークン予算による教師信号
ヒントのサイズの教師信号は、複数の粒度で候補ヒントを評価して得るねん。トークン予算付きのLLM呼び出しを使うんよ。
各学習クエリqに対して、まずLLMを1回呼び出して参照用の完了文 $h_l(q)$ を取得して、そのLLMトークンの長さ $|h_l(q)|$ を使ってパーセンテージサイズ p ∈ {0, 10, 20, ..., 90} を定義するんや。
なんで10%刻みにしてるかっていうと、ヒントトークンの非滑らかな効果曲線をちゃんと捉えられるくらいの細かさがありつつ、計算コスト的にも現実的やからやねん。もっと細かく5%刻みにしたら、ラベリングコストが2倍になるのに「最小限で十分なサイズ」を見つける精度はそんなに上がらへん。逆に25%刻みとか粗くしすぎると、ヒントが効き始める重要な転換点を見逃すリスクがあるんよ。
各pに対して、目標トークンサイズをこう計算するねん:
$n_p = \lfloor \frac{p}{100} |h_l(q)| \rfloor$
ほんで、max_new_tokensパラメータを $n_p$ に設定してLLMを再度呼び出すんや。このパラメータは生成長のハード制約として働いて、モデルが事前定義されたサイズ $n_p$ に収まる完了文 $h_l^{(n_p)}(q)$ を出力するようにするねん。
このサイズ制約付きの完了文を候補ヒント hint(q, $n_p$) = $h_l^{(n_p)}(q)$ として扱って、SLMを q ⊕ hint(q, $n_p$) で実行して $\phi(q, h_s(q \oplus \text{hint}(q, n_p)))$ を計算することで評価するんよ。
離散化された最小十分サイズはこう記録するで:
$n^*(q) = \min \{n_p : \phi(q, h_s(q \oplus \text{hint}(q, n_p))) \geq \tau \}$
これは連続的な最適解のグリッドベースの近似やねん。p = 0 の場合は hint(q, 0) = ∅ に対応してて、つまりルーターがLLMにヒントを全く求めずに、SLMの出力 $h_s(q)$ をそのまま返すってことや。p = 90 までの部分サイズのどれも閾値を満たさへん場合は、$n^*(q) = |h_l(q)|$ に設定して、LLMの完全な応答を出力として使うねん。
設計選択の根拠
**10%の粒度について**
10%刻みの選択は、ラベリング効率と精度のバランスを取ってるねん。各学習クエリには |{0, 10, 20, ..., 90}| = 10回のLLM呼び出しが必要で、教師信号を構築するんや。もっと細かい粒度にしたら $n^*(q)$ のちょっとマシな近似が得られるけど、計算コストがめっちゃ高くなる——5%刻みやと1クエリあたり20回の呼び出しが必要で、ラベリング予算が倍になってまうねん。逆に、粗い粒度(例えば25%刻み)やと、ヒントが十分になる重要な転換点を見逃すリスクがあるんよ。特に品質が急激に変化するクエリでは問題やな。
**決定論的LLMデコーディングについて**
ヒントラベリングの全LLM呼び出しでは、決定論的デコーディング(temperature=0、top_p=1)を使ってるねん。なんでかっていうと、再現可能な教師信号を確保して、異なる学習ランでのサンプリングによる分散を排除するためや。この設計選択は、ヒント内容の多様性よりも学習ラベルの一貫性を優先してるってことやな。
---
## Page 12
[](/attach/4f91145b287ae51d50fb00db9c73a1abd8c4abfaa816d614e134c6b64fbc173e_p012.png)
### 和訳
LLMシェパーディング
**グリッドベースの近似について**
離散化したターゲットn∗(q)っていうのは、連続的な最適解の代わりに使う実用的な代理変数やねん。これ使うと量子化誤差が出てまうんやけど、10%刻みのグリッドで十分やねん。なんでかっていうと、クエリごとにヒントがどんだけ必要かの違いをちゃんと捉えられるからや。しかも回帰のターゲットを対数変換してる(セクション3参照)から、細かい離散化のノイズもええ感じに滑らかになるんよ。
**B.2. 最適化と実装の詳細**
学習にはAdamW(Loshchilov & Hutter, 2019)使ってて、評価とチェックポイント選択用にパラメータの指数移動平均(EMA)を保持してるで(Morales-Brotons et al., 2024)。
**クラスバランシング**
クラスの偏りがあるかもしれへん状況(つまりヒントが必要なクエリの割合が50%からずれてる場合やな)では、WeightedRandomSamplerっていうのを学習中に使って、ミニバッチの分布をバランスよくしてるねん。こうすることで、正例も負例も各勾配更新でちゃんと代表されるようになって、頑健な決定境界が得られるっちゅうわけや。
**ポリシーのキャリブレーション**
学習が終わった後、検証セットでグリッドサーチして、目標のコストサイズに合わせてポリシーをキャリブレーションするねん。具体的には、固定のコスト制約Ctargetが与えられたとき、二値分類の判定に使う確率閾値αを探索して、コスト制約を満たしながら検証精度を最大化する設定を見つけるんや。これで再学習せんでも、学習済みモデルを色んなコスト-精度のトレードオフに適応させられるっちゅうことやな。
**C. 外れ値分析**
**C.1. 外れ値の検出戦略**
学習データセットの外れ値を見つけてフィルタリングするために、異なるヒントサイズ間での一致パターンを利用した合意ベースのアプローチを使ってるねん。各サンプルについて、11種類のヒントサイズ設定でSLM(小規模言語モデル)の応答を生成して、正解と比較するんや。各ヒントサイズのレベルで、少数派のクラス(正解か不正解か)が出たらそれを外れ値として分類して、そうでなければ正常とするねん。ほんでこの二値の外れ値フラグを集計して、サンプルごとに全ヒントサイズ設定での外れ値の総数kを計算するんよ。
外れ値カウントが高いサンプル(例えばk ≥ 閾値)は、ヒントサイズが変わると挙動が一貫してへんから、学習中にノイズになる可能性があるねん。やから、そういうサンプルはフィルタリングしてデータセットの品質を上げるっちゅうわけや。図4と図5は、CNK12とGSM8Kデータセットの外れ値カウントの分布を示してるで。
図4. CNK12データセットの外れ値分布
注意点として、この外れ値フィルタリング戦略はCNK12とGSM8Kにだけ適用してるねん。なんでかっていうと、これらのデータセットは統計的フィルタリングを正当化できるだけの十分な学習サンプルがあるからや。HumanEvalは評価専用に設計された165問しかないから、外れ値分析はやってへん。同様に、MBPPデータセットも学習セットに374サンプルしかなくて、これ以上サンプル減らしたら学習データのサイズがめっちゃ小さくなってまうから、HumanEvalやMBPPには外れ値フィルタリングは適用してへんねん。
---
## Page 13
[](/attach/4f91145b287ae51d50fb00db9c73a1abd8c4abfaa816d614e134c6b64fbc173e_p013.png)
### 和訳
LLMシェファーディング
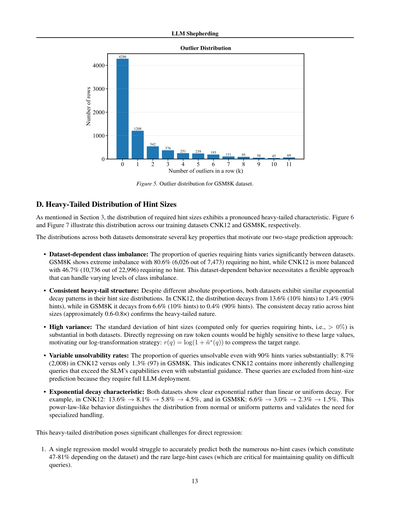
図5. GSM8Kデータセットの外れ値の分布やで。
D. ヒントサイズのヘビーテール分布について
セクション3でも言うたけど、必要なヒントサイズの分布ってめっちゃ偏っとんねん。いわゆる「ヘビーテール」ってやつや。図6と図7は、CNK12とGSM8Kっていう2つのトレーニングデータセットでこの分布がどうなってるか見せとるで。
両方のデータセットの分布見たら、ワイらが「2段階予測アプローチ」を採用した理由がわかる特徴がいくつかあんねん:
• データセットによってクラスの偏りが全然違う:ヒントが必要なクエリの割合がデータセットによってめっちゃ違うんや。GSM8Kはえげつない偏りがあって、7,473件中6,026件、つまり80.6%がヒントいらんねん。一方CNK12はもうちょいバランスよくて、22,996件中10,736件、46.7%がヒント不要や。こんな感じでデータセットごとに挙動が違うから、いろんなレベルのクラス不均衡に対応できる柔軟なアプローチが必要やったわけや。
• 一貫したヘビーテール構造:絶対的な割合は違っても、両方のデータセットでヒントサイズの分布は似たような指数関数的な減衰パターンを見せとんねん。CNK12では13.6%(10%ヒント)から1.4%(90%ヒント)に減少して、GSM8Kでは6.6%(10%ヒント)から0.4%(90%ヒント)に減少しとる。ヒントサイズ間の減衰率が大体0.6〜0.8倍で一定やから、ヘビーテールの性質が確認できるわけや。
• 分散がデカい:ヒントが必要なクエリ(つまり0%より大きいやつ)だけで計算したヒントサイズの標準偏差がどっちのデータセットでもかなりデカいんや。生のトークン数をそのまま回帰しようとしたら、こういうデカい値にめっちゃ敏感になってまうねん。やから対数変換っていう戦略を使ったんや:r(q) = log(1 + ˜n∗(q)) で目標範囲を圧縮するっちゅうことやな。
• 解けへん問題の割合も違う:90%のヒントあげても解けへんクエリの割合もデータセットで結構違うんや。CNK12では8.7%(2,008件)やけど、GSM8Kではたった1.3%(97件)やねん。つまりCNK12には、めっちゃガイダンスあげてもSLM(小さい言語モデル)の能力超えてまうような、本質的にムズい問題がもっと含まれとるってことや。こういうクエリはフルでLLM使わなあかんから、ヒントサイズ予測からは除外しとるで。
• 指数関数的減衰の特徴:両方のデータセットで、線形とか一様とかちゃうて、はっきり指数関数的な減衰が見られんねん。例えばCNK12では13.6% → 8.1% → 5.8% → 4.5%で、GSM8Kでは6.6% → 3.0% → 2.3% → 1.5%や。このべき乗則みたいな振る舞いが、正規分布とか一様分布とは違うってことを示しとって、特別な扱いが必要やってことを裏付けとるんや。
このヘビーテール分布は直接回帰するにはめっちゃ厄介な課題があんねん:
1. 単一の回帰モデルやと、ヒント不要のケース(データセットによって47〜81%もあるやつ)と、レアな大きいヒントが必要なケース(難しいクエリの品質維持にめっちゃ重要なやつ)の両方を正確に予測するんはキツいんや。
---
## Page 14
[](/attach/4f91145b287ae51d50fb00db9c73a1abd8c4abfaa816d614e134c6b64fbc173e_p014.png)
### 和訳
LLMシェパーディング
図6. CNK12データセット(22,996件のクエリ)における最小必要ヒントサイズの分布やねん。
2. 普通のℓ2損失(二乗誤差のことやな)使うと、テール部分の再構成誤差にめっちゃ引っ張られてまうねん。そしたら、もっとよく出てくる短いヒントの場合の精度が犠牲になってまう可能性があるわけや。
3. データセットによってクラスのバランスがバラバラやねん(CNK12では47対53やけど、GSM8Kでは81対19や)。せやから、重み付きサンプリングで柔軟に対応せなあかんねん。そうすることで、いろんなデータ分布でもちゃんとした決定境界が作れるようになるわけや。
4. 解けへんクエリも存在するねん(データセットによって1.3〜8.7%くらいや)。これを明示的に処理せなあかん。なんでかっていうと、そもそも無理なケースにヒントを予測しようとするのを避けるためやねんな。
ワイらの2段階アプローチ—まずヒントが必要かどうかを分類して、その後で正のケースだけサイズを予測する—は、この難しい分布をもっと扱いやすい2つのサブ問題に自然に分解してくれるねん。1つ目は、バランスのとれた二値分類や(データセット特有の偏りに適応する重み付きサンプリング使うで)。2つ目は、条件付き分布p(n∗|n∗ > 0)に対する回帰やねん。これはまだヘビーテールやけど、支配的なゼロの部分を除外して、連続的なヒントサイズの範囲にモデルの容量を集中できるんや。この分解は、難易度プロファイルが異なるデータセット間でもほんまに頑健やで。バランスのとれたCNK12と偏りのあるGSM8Kの両方で一貫したパフォーマンスが出とることからも、それがわかるわな。
E. プロンプティングの詳細
このセクションでは、大規模モデルでのヒント生成、小規模モデルでの推論、そしてシェパーディング監督に使われる詳細なプロンプト手順を説明するで。
E.1. プロンプトテンプレート
全データセットを通じて、小規模モデルも大規模モデルも同じ指示付きでクエリを受け取るねん。で、利用可能な場合は、生成された大規模モデルのヒントを追加の文脈入力として受け取るわけや。一般的なプロンプト構造はこんな感じや:
指示:タスク固有の制約に従って最終回答を出してな。
質問:{クエリ}
ヒント:{生成された大規模モデルの出力}
ヒントが提供されへん場合は、「ヒント:」の行が省略される以外は同じプロンプトやで。
GSM8K:2つの例題(質問と回答のペア)からなる固定のfew-shotプロンプトを使うて、その後にターゲットのクエリを続けるねん。利用可能な場合は、生成された大規模モデルのヒントが追加の文脈として付け加えられるで。
14
---
## Page 15
[](/attach/4f91145b287ae51d50fb00db9c73a1abd8c4abfaa816d614e134c6b64fbc173e_p015.png)
### 和訳
LLMシェファーディング
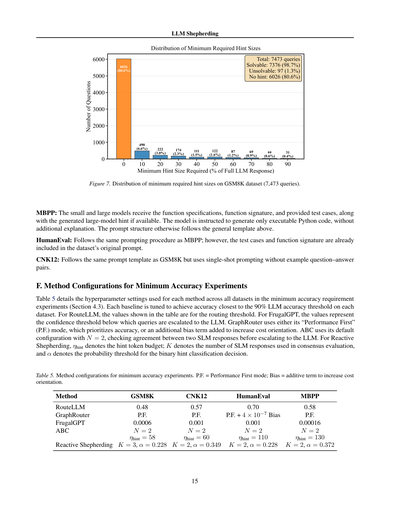
図7. GSM8Kデータセット(7,473件のクエリ)での最小ヒントサイズの分布やで。
MBPP: 小さいモデルと大きいモデルには、関数の仕様、関数のシグネチャ(引数とか戻り値の型とかやな)、用意されたテストケースが渡されるねん。で、大きいモデルからのヒントがあったらそれも一緒に渡される。モデルには「余計な説明なしで、実行できるPythonコードだけ出してな」って指示するわけや。プロンプトの構造は、それ以外は上で説明した一般的なテンプレートと同じやで。
HumanEval: MBPPと同じプロンプトの手順に従うんやけど、テストケースと関数シグネチャはデータセットの元のプロンプトに最初から入ってるねん。
CNK12: GSM8Kと同じプロンプトテンプレート使うんやけど、例題の質問と回答のペアなしの「シングルショットプロンプティング」(一発勝負みたいなもんやな)でやるねん。
F. 最小精度実験のための各手法の設定
表5は、最小精度要件の実験(セクション4.3参照)で全データセットに対して使った各手法のハイパーパラメータ設定を詳しく示してるで。各ベースライン手法は、それぞれのデータセットで90%のLLM精度閾値にできるだけ近い精度を達成するようにチューニングしてあるねん。RouteLLMの場合、表に載ってる値はルーティング閾値や。FrugalGPTの場合は、「この自信度より低かったらLLMにエスカレーションする」っていう信頼度閾値を表してるねん。GraphRouterは「Performance First」(P.F.)モードっていう精度優先のモードを使うか、コスト重視を強めるためのバイアス項を追加するかのどっちかや。ABCはデフォルト設定のN=2を使ってて、これは2つのSLM(小さいモデル)の回答が一致するかチェックして、一致せえへんかったらLLMにエスカレーションするっていう仕組みやねん。Reactive Shepherdingについては、ηhintはヒントトークンの予算、KはコンセンサスSLM評価で使うSLMの回答数、αはバイナリヒント分類(ヒント出すか出さんかの判断やな)の確率閾値やで。
表5. 最小精度実験の各手法設定。P.F. = Performance Firstモード、Bias = コスト重視を強めるための加算項。
| 手法 | GSM8K | CNK12 | HumanEval | MBPP |
|------|-------|-------|-----------|------|
| RouteLLM | 0.48 | 0.57 | 0.70 | 0.58 |
| GraphRouter | P.F. | P.F. | P.F. + 4×10⁻⁷ Bias | P.F. |
| FrugalGPT | 0.0006 | 0.001 | 0.001 | 0.00016 |
| ABC | N = 2 | N = 2 | N = 2 | N = 2 |
| Reactive Shepherding | ηhint = 58, K = 3, α = 0.228 | ηhint = 60, K = 2, α = 0.349 | ηhint = 110, K = 2, α = 0.228 | ηhint = 130, K = 2, α = 0.372 |
---
## Page 16
[](/attach/4f91145b287ae51d50fb00db9c73a1abd8c4abfaa816d614e134c6b64fbc173e_p016.png)
### 和訳
G. その他の関連研究
LLMシェパーディング
効率よく、正確に、ほんでコストも抑えたSLM-LLM協調推論のための既存テクニックには、こんなんがあるねん:1) LLMルーティング、2) LLMカスケーディング、3) 投機的デコーディング、4) 知識蒸留や。
G.1. LLMルーティング
LLMルーティングっちゅうのは、コストと品質のトレードオフに対処するために、学習済みのルーターを使って「このクエリはどのモデルに任せたらええか」を事前に決める手法やねん。Luらの初期の研究(Lu et al., 2024)では「Zooter」っちゅう報酬ガイド型ルーティング手法を提案しとって、訓練クエリから報酬を蒸留してルーティング関数を学習することで、26個のベンチマークサブセットのうち44%のタスクでトップ性能を達成しつつ、計算効率も維持したんや。これを土台にして、Hybrid-LLM(Ding et al., 2024)は品質を意識したクエリルーティングを提案したんやけど、これは予測されるクエリの難易度に基づいて品質とコストを動的にトレードオフするもんで、品質を落とさずに大規模モデルへの呼び出しを最大40%も減らせたんやで。RouterBench(Hu et al., 2024)はその後、代表的なLLMから40万5千件以上の推論結果を集めた標準化評価フレームワークを確立して、ルーティング戦略を体系的に比較できるようにしたんや。RouteLLM(Ong et al., 2025)は人間の好みデータからルーターを学習するための原理的なフレームワークを導入して、MT-Benchで85%以上、GSM8Kで35%のコスト削減を達成しながら、GPT-4の性能の95%を維持することを実証したんや。ほんで最近では、GraphRouter(Feng et al., 2025)が帰納的グラフフレームワークを提案しとって、タスク・クエリ・LLM間の文脈的相互作用をヘテロジニアスグラフとしてモデル化することで、先行するルーターより少なくとも12.3%の改善と、未知のLLMへの汎化能力向上を達成したんやで。
これらの進歩があったとはいえ、ルーティングには根本的な構造上の限界があんねん:なんでかっていうと、決定が本質的に二択(SLMかLLMか)やから、LLMが選ばれたらシステムは推論コストを丸ごと負担せなあかんねん。ルーティングはLLMの知識の部分的な再利用を促進せえへんから、厳格なコスト制約には十分柔軟やないんや。
G.2. LLMカスケーディング
LLMカスケーディングは、モデルを階層的に配置して、弱いモデルが品質基準を満たせへん時に、より高性能なモデルにクエリをエスカレーションする手法やねん。FrugalGPT(Chen et al., 2024)がこのアプローチの先駆けで、クエリごとにどのLLMの組み合わせを使うかを学習することで最大98%のコスト削減を実証したんや。LLM-Blender(Jiang et al., 2023)はアンサンブルの観点を導入して、ペアワイズランキングで候補出力から選択し、生成的融合でトップ候補をマージするようにしたんや。AutoMix(Aggarwal et al., 2024)は少数ショット自己検証とPOMDPベースのルーティングでカスケーディングを進化させて、コストを50%以上削減したんやで。最近の研究では学習型と訓練不要型の両方のアプローチが探求されとって:C3PO(Chen et al., 2025)は正式なコスト保証付きのラベル不要カスケーディングを提供し、Agreement-Based Cascading(ABC)(Kolawole et al., 2025)はモデル応答のアンサンブル間の合意に基づいてエスカレーション判断を行うシンプルで訓練不要な戦略を提案しとるんや。ワイらの単一SLM設定では、同じSLMからの複数の応答間の合意を測定することでABCを適応させとるで。
カスケーディングは平均コストを削減できるけど、厳格な予算制約には向いてへんねん:なんでかっていうと、SLMは複雑なタスクでよう失敗して、完全なLLM推論がトリガーされてまうからや。エスカレーションのたびに完全なLLMフォワードパスが必要やから、SLMの信頼性が低いとコスト削減が限られてまうんや。
G.3. 投機的デコーディング
投機的デコーディング(Leviathan et al., 2023; Chen et al., 2023)は、出力品質を犠牲にせずにLLM推論を高速化するために広く採用されとるテクニックやねん。このアプローチでは、小さいドラフトモデルを使って候補トークン列を生成して、それを大きいターゲットモデルが並列で検証するんや。ターゲットモデルの分布と一致するトークンは受け入れられて、大規模モデル推論のコストを複数トークンにわたって償却できるんやで。Medusa(Cai et al., 2024)はこのアイデアを拡張して、LLM自体に複数のデコーディングヘッドを追加することで、別のドラフトモデルの必要性をなくしたんや。Draft & Verify(Zhang et al., 2024)はドラフト作成中に中間層を選択的にスキップすることで自己投機的デコーディングを実現して、追加訓練なしで最大2倍のスピードアップを達成したんや。Online Speculative Decoding(Liu et al., 2024)は推論中にドラフトモデルを継続的に適応させてトークン受理率を向上させるんやで。
投機的デコーディングとシェパーディングはどっちも小さいモデルと大きいモデルの協調を含むけど、その目的は根本的に違うねん。投機的デコーディングはトークン検証を並列化してLLM推論を高速化することが目的やけど、大きいモデルはすべての出力トークンのチェックに関与したままなんや。それに対してシェパーディングは、SLMが部分的なLLMガイダンスだけで最終応答を生成することで、LLMの使用を最小化することが目的やねん。
---
## Page 17
[](/attach/4f91145b287ae51d50fb00db9c73a1abd8c4abfaa816d614e134c6b64fbc173e_p017.png)
### 和訳
G.4. 知識蒸留(Knowledge Distillation)
LLMシェパーディング
知識蒸留(KD)っていうのはな(Hintonらが2015年に提唱したやつやねん)、でっかい先生モデルから小さい生徒モデルに、トレーニング中に能力を移し替える技術やねん。最近はこのKDがLLM(大規模言語モデル)にも応用されとってな、MiniLLM(Guら、2024年)は「逆KLダイバージェンス」っていう蒸留の目的関数を提案しとるねん。これがめっちゃ生成型の言語モデルに向いとるんやけど、なんでかっていうと、生徒モデルが確率低いところを過大評価してまうのを防いでくれるからやねん。それからDistilling Step-by-Step(Hsiehら、2023年)はな、LLMから「こうやって考えたで」っていう思考の過程(chain-of-thought rationales)を抜き出して、小さいモデルをより少ないデータで効率よく訓練できるようにしたんや。これがほんまにすごくてな、たった7億7千万パラメータのモデルが、5400億パラメータのPaLMを少数例プロンプトで使った時よりも良い成績出せるようになったんやで。詳しい総説(Gouら、2021年;Xuら、2024年)では、特定スキル向けとか特定ドメイン向けの蒸留も含めて、LLM向けKD技術を幅広くカバーしとるで。
知識蒸留とシェパーディングは補完し合う関係やけど、全然別もんやねん。KDはトレーニング時の技術やから、蒸留が終わったら生徒モデルは推論時に独立して動くんや。一方でシェパーディングは推論時のコラボレーションで、クエリの難しさに応じてLLMからのヒントを動的に注入するんやで。KDはSLM(小規模言語モデル)の基礎能力を底上げするもんで、シェパーディングはその基礎能力じゃ足らん時にピンポイントでアシストしてくれるもんなんや。
G.5. LLMシェパーディングの位置づけ
ワイらの研究は、上で挙げた全部のアプローチと根本的に違うんやで。ルーティングやカスケーディングは「どっちのモデルに完全な回答を作らせるか」っていう二者択一の判断をするやろ?でもシェパーディングは「LLMからどれだけ出力をもらうか」をコントロールできるから、コストと品質の間で連続的なトレードオフができるんや。スペキュラティブデコーディングとも違うでな。あれはLLM推論を高速化するけど、全てのトークンでLLMがクリティカルパスに入っとるやろ?シェパーディングは最終的な回答生成からLLMを完全に外してまうんや。知識蒸留とも違うで。あれはトレーニング時に働くもんやけど、シェパーディングは推論時にクエリごとに動的なガイダンスを提供するんやで。
シェパーディングは既存のアプローチを補完できるんや。プロアクティブ・シェパーディングはルーティングを強化して、LLMのフル呼び出しを部分的なヒントに置き換えるし、リアクティブ・シェパーディングはカスケーディングを強化して、完全なエスカレーションをピンポイントのガイダンスに置き換えるんや。それに蒸留済みのSLMと組み合わせたらさらに改善できるで。ワイらが知る限り、SLMとLLMのコラボレーションでトークンレベルの予算コントロールを活用した研究はこれが初めてやねん。
---
![]()
1 / 1

